Cảm ơn bạn Sphinx đã giải thích đầy đủ các vấn đề nêu ra ở trên. Tôi chỉ xin tóm lược lại và diễn giải một chút để tìm các hàm truyền mà bạn Sphinx đã trình bày.
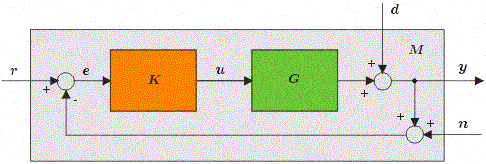
Các bạn xem lại hình thevane006 ở trên (được đánh số theo nick của tôi + số thứ tự của hình để không nhầm với hình của các bạn khác gửi). Nếu ta không quan tâm đến các đầu vào n và r thì có thể vẽ lại như hình sau.

Hình - thevane008
Lưu ý nút cộng đại số

biểu diễn y = d + n

biểu diễn y = d – n.
Ta có thể tính hàm truyền từ d đến y như sau:
y = d + z
mà z = G*K*e = G * K * (-y) = - G*K*y
Lưu ý dấu trừ trên hình thevane006.
=> y = d - G*K*y
=> y(1 + G*K) = d
Nếu ký hiệu L = G*K và hàm truyền từ d đến y là S ta có
y = 1 / (1 + GK) * d = 1/ (1 + L) * d = S * d
=> S = 1/ (1 + L)
Tính tương tự hàm truyền từ r đến e, không quan tâm đến các đầu vào d và n ta có hình sau.

Hình - thevane009
Ta cũng có
e = r – z = r - G*K*e = r – L*e
=> e(1 +L) = r
=> e = 1/(1 + L) * r = S * r
Như vậy, hàm truyền từ d đến y cũng bằng hàm truyền từ r đến e và bằng S. Hàm này đánh giá độ nhạy của đầu ra y đối với đầu vào d hay độ nhạy của đầu ra e với đầu vào r.
Nếu ký hiệu hàm truyền từ r đến y là T thì, với cách tính tương tự như trên, các bạn có thể dễ dàng suy ra được hàm truyền này bằng
T = L / (1 + L)
Hàm này đánh giá độ nhạy của đầu ra y đối với đầu vào r.
Vì ta có thể dễ dàng suy ra được T + S = 1 nên theo định nghĩa ở trên thì có thể coi T là hàm bù nhạy của y (hay e) với d (hay r). Ngược lại, S là hàm bù nhạy của y với r.
Trong thực tế người ta thường quan tâm đến độ nhạy của đầu ra y với đầu vào d nên khi nói “độ nhạy” của hệ thống người ta ngầm hiểu là nói đến S. Vì vậy S được nói ngắn gọn là hàm độ nhạy và T được gọi là hàm bù nhạy của S.
Ở trên bạn Sphinx viết T=L/(1+L) gọi là hàm nhạy. S=1/(1+L) gọi là hàm bù nhạy cũng không có gì mâu thuẫn với những điều vừa nói vì bạn không chỉ rõ T là hàm độ nhạy của đầu ra nào với đầu vào nào. Tuy nhiên, chúng ta sẽ thống nhất từ nay trở đi, nếu chỉ nói "hàm độ nhạy" mà không có chú thích gì thêm thì ta hiểu là S và T làm bù nhạy.
Ghi chú thêm (các bạn mới học không cần hiểu phần này): Nguyên gốc của từ “độ nhạy” không phải được hiểu với ý nghĩa như trên. Bản chất của nó được bắt nguồn từ chỗ: mô hình toán học mô tả đối tượng cần điều khiển thường không thể phản ánh được hết bản chất vật lý của đối tượng thực và thường có sự sai lệch nhất định. Vì vậy Bode đưa ra khái niệm này để đánh giá mức độ nhạy cảm của hàm truyền đạt hệ kín T = L /(1+L) khi có sự không chính xác trong mô hình hàm truyền đạt của đối tượng (xem thêm cuốn “lý thuyết điều khiển tuyến tính” của Nguyễn Doãn Phước, NXB KHKT Hà nội 2002, trang 257). Để đánh giá mức độ nhạy cảm này người ta lấy đạo hàm của hàm truyền hệ kín T theo hàm truyền của đối tượng G (vì không gõ được công thức nên tôi cũng học tập bạn Sphinx gửi ảnh của nó, các bạn xem hình dưới đây).

Các hình trên được đính kèm phía dưới đây để đề phòng trường hợp bị mất hình. Thứ tự là:
- thevane008
- thevane009
- thevane_congthuc_001
Các bạn xem lại hình thevane006 ở trên (được đánh số theo nick của tôi + số thứ tự của hình để không nhầm với hình của các bạn khác gửi). Nếu ta không quan tâm đến các đầu vào n và r thì có thể vẽ lại như hình sau.

Hình - thevane008
Lưu ý nút cộng đại số

biểu diễn y = d + n

biểu diễn y = d – n.
Ta có thể tính hàm truyền từ d đến y như sau:
y = d + z
mà z = G*K*e = G * K * (-y) = - G*K*y
Lưu ý dấu trừ trên hình thevane006.
=> y = d - G*K*y
=> y(1 + G*K) = d
Nếu ký hiệu L = G*K và hàm truyền từ d đến y là S ta có
y = 1 / (1 + GK) * d = 1/ (1 + L) * d = S * d
=> S = 1/ (1 + L)
Tính tương tự hàm truyền từ r đến e, không quan tâm đến các đầu vào d và n ta có hình sau.

Hình - thevane009
Ta cũng có
e = r – z = r - G*K*e = r – L*e
=> e(1 +L) = r
=> e = 1/(1 + L) * r = S * r
Như vậy, hàm truyền từ d đến y cũng bằng hàm truyền từ r đến e và bằng S. Hàm này đánh giá độ nhạy của đầu ra y đối với đầu vào d hay độ nhạy của đầu ra e với đầu vào r.
Nếu ký hiệu hàm truyền từ r đến y là T thì, với cách tính tương tự như trên, các bạn có thể dễ dàng suy ra được hàm truyền này bằng
T = L / (1 + L)
Hàm này đánh giá độ nhạy của đầu ra y đối với đầu vào r.
Vì ta có thể dễ dàng suy ra được T + S = 1 nên theo định nghĩa ở trên thì có thể coi T là hàm bù nhạy của y (hay e) với d (hay r). Ngược lại, S là hàm bù nhạy của y với r.
Trong thực tế người ta thường quan tâm đến độ nhạy của đầu ra y với đầu vào d nên khi nói “độ nhạy” của hệ thống người ta ngầm hiểu là nói đến S. Vì vậy S được nói ngắn gọn là hàm độ nhạy và T được gọi là hàm bù nhạy của S.
Ở trên bạn Sphinx viết T=L/(1+L) gọi là hàm nhạy. S=1/(1+L) gọi là hàm bù nhạy cũng không có gì mâu thuẫn với những điều vừa nói vì bạn không chỉ rõ T là hàm độ nhạy của đầu ra nào với đầu vào nào. Tuy nhiên, chúng ta sẽ thống nhất từ nay trở đi, nếu chỉ nói "hàm độ nhạy" mà không có chú thích gì thêm thì ta hiểu là S và T làm bù nhạy.
Ghi chú thêm (các bạn mới học không cần hiểu phần này): Nguyên gốc của từ “độ nhạy” không phải được hiểu với ý nghĩa như trên. Bản chất của nó được bắt nguồn từ chỗ: mô hình toán học mô tả đối tượng cần điều khiển thường không thể phản ánh được hết bản chất vật lý của đối tượng thực và thường có sự sai lệch nhất định. Vì vậy Bode đưa ra khái niệm này để đánh giá mức độ nhạy cảm của hàm truyền đạt hệ kín T = L /(1+L) khi có sự không chính xác trong mô hình hàm truyền đạt của đối tượng (xem thêm cuốn “lý thuyết điều khiển tuyến tính” của Nguyễn Doãn Phước, NXB KHKT Hà nội 2002, trang 257). Để đánh giá mức độ nhạy cảm này người ta lấy đạo hàm của hàm truyền hệ kín T theo hàm truyền của đối tượng G (vì không gõ được công thức nên tôi cũng học tập bạn Sphinx gửi ảnh của nó, các bạn xem hình dưới đây).

Các hình trên được đính kèm phía dưới đây để đề phòng trường hợp bị mất hình. Thứ tự là:
- thevane008
- thevane009
- thevane_congthuc_001






























Comment